Jupyter notebooks in Python

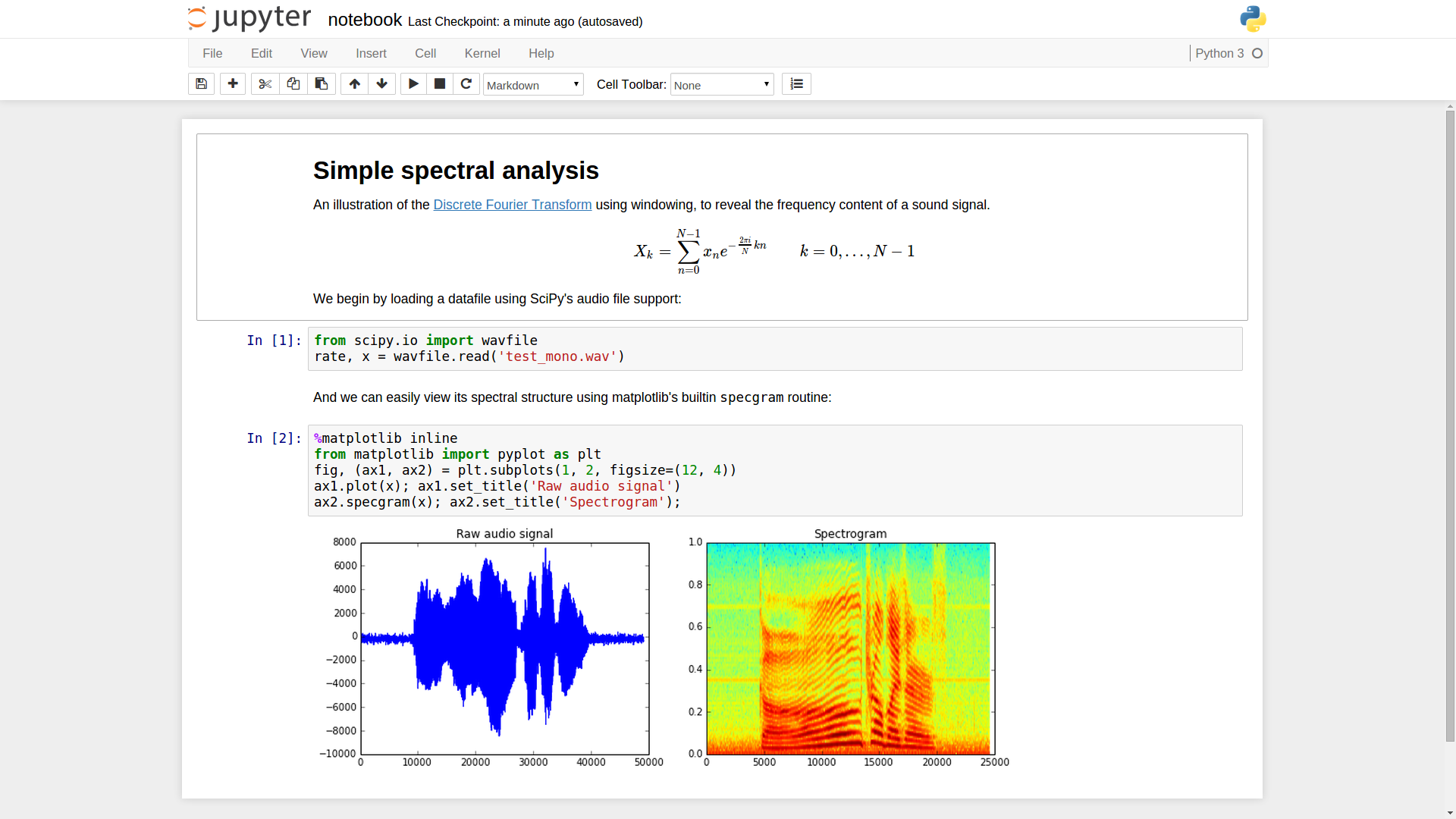
How to use Jupyter?

• Jupyter is included in the Anaconda distribution
  • Start Anaconda from menu or run anaconda-navigator on command line
  • Install the Jupyter Notebook application in Anaconda
  • If it’s already installed, click on Launch to start it
  • JupyterLab provides an integrated environment, similar to R Studio or Matlab
• Without installing, online notebooks are available at Google Colab , DeepNote , and Azure Notebooks
• Try notebooks in your browser:
  • Live intro notebook

Block execution

Follow sections on the official Notebook Examples tutorial:

• Structure of notebook documents
• Kernels, cell types: markdown vs code
• Navigation, running code
• Order of execution

Practice! Open a Jupyter notebook and follow along

Do ONE of the following:

1. Open online notebook at Google Colab , DeepNote , or Azure Notebooks
2. Or download Anaconda and run Jupyter Notebook or JupyterLab
3. Use Visual Studio Code with its regular Python extension
4. Use JupyterLite (doesn’t save across browsers or computers - not a cloud service!)

Python’s Numpy module

From Python for Data Analysis, 2nd Ed, chapter 4 :

• enables working with $n$-dimensional arrays
• math functions without needing to loop over arrays
• 10-100x faster than using regular Python
• reading/writing to files
• advanced math: linear algebra, random numbers, etc

How do dimensions work?

1 dimension: 1 bracket, 1 index

arr1d = np.array([1, 2, 3])
arr1d[x]

arr2d = np.array([[1, 2, 3],
                  [4, 5, 6]])
arr2d[x, y]

arr3d = np.array([[[ 1,  2,  3],
                   [ 4,  5,  6]],
                  [[ 7,  8,  9],
                   [10, 11, 12]]])
arr3d[x, y, z]

Numpy overview

• Creating and manipulating ndarray objects and doing math on them
• Data types for efficient storage and use
• Indexing and slicing; with boolean expressions and fancy indexing
• Unary and binary math functions

Numpy practice

Start by working in teams on the whiteboard and
then submit individually by forking this or create an online notebook.

Option 1

Solve ONE of these problems (thanks math people!):

1. Largest product in a grid
2. Maximum path sum II
3. Non-abundant sums
4. Lexicographic permutations

Make sure to:

• Use numpy arrays and arithmetic operations in page below

Option 2

Do 3 examples of each below and briefly explain each with one sentence:

• Create numpy arrays in 1D, 2D, and 3D
• Index slices in 1D, 2D, and 3D
• Do some arithmetic
• Use Boolean indexing

Linear algebra basics:

Vectors and matrices

Basics: Vectors

Vectors: $\vec{x} = [ 1, 2, 3 ]$

• Why? Most data comes in vectors

Can do bulk operations using math magic:

• Adding or subtracting a scalar: $$ \vec{x} + 1 = [ 2, 3, 4 ] $$
• Multiplying or dividing by a scalar: $$ \vec{x} \times 2 = [ 2, 4, 6 ] $$
• Adding two vectors (of same size): $$ \vec{x} + \vec{x} = [ 2, 4, 6 ] $$

Vector math: dot product

inner/dot product : $$ \vec{x} \cdot \vec{y} = \sum x_i y_i $$

• Calculates “length of projection” in geometric sense
• Multiply corresponding elements and sum to result in scalar
• Useful in calculating weighted sums, scaling data elements, etc.

quantity = np.array([1, 1, 5, 2])
prices = np.array([10, 15, 1.25, 20])
total = np.dot(prices, quantity)

Vector math: outer product

(definition)

$$ \vec{x} \times \vec{y} = [x_i y_j]_{ij} $$

• element-by-element multiplication, results in $ n \times m $ size matrix
• useful when duplicating rows or columns, or scaling them

item_prices = np.full((1,5), 50) # all $50
inflation_per_month = np.array([1.1, 1.3, 1.3, 1.4]) # monthly inflation
new_prices_per_month = np.outer(inflation_per_month, item_prices)

array([[55., 55., 55., 55., 55.],
       [65., 65., 65., 65., 65.],
       [65., 65., 65., 65., 65.],
       [70., 70., 70., 70., 70.]])

Basics: Matrices

$$ A=\left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \newline \vdots & \ddots & \vdots \newline a_{m1} & \cdots & a_{mn} \newline \end{array} \right] $$

Uses:

• Aggregation of many vectors
• Bases for transformation spaces
• Image data and manipulation

Matrix multiplication

Must have matching inner dimensions, results in a matrix: $$ A_{m\times n} \times B_{n\times o} = C_{m\times o} $$

Each element of output matrix is the result of one inner product: $$ c_{ij} = \sum_k a_{ik} b_{kj} $$

Rows of $A$ matched to columns of $B$ to create single elements of $C$: $$ \left[ \begin{array}{c} \bbox[5px,yellow,border:2px solid red]{\begin{array}{ccc} a_{11} & \cdots & a_{1n} \end{array}} \newline \begin{array}{ccc} \vdots & \ddots & \vdots \newline a_{m1} & \cdots & a_{mn} \newline \end{array} \end{array} \right] \times \left[ \begin{array}{cc} \bbox[5px,yellow,border:2px solid red]{\begin{array}{c} b_{11} \newline \vdots \newline b_{n1} \end{array}} & \begin{array}{cc} \cdots & b_{1o} \newline \ddots & \vdots \newline \cdots & b_{no} \newline \end{array} \end{array} \right] = \left[ \begin{array}{ccc} \bbox[5px,yellow,border:2px solid red]{c_{11}} & \cdots & c_{1o} \newline \vdots & \ddots & \vdots \newline c_{m1} & \cdots & c_{mo} \newline \end{array} \right] $$

Uses of matrix algebra

• Useful transforming rows of data, image operations, 3D rotations, machine learning, etc.
• Google’s PageRank algorithm is:

  […] calculated using a simple iterative algorithm, and corresponds to the principal eigenvector of the normalized link matrix of the web. (from original paper )

• Inverse of a matrix can be calculated to satisfy: $$ A\times A^{-1} = I$$
• Solving linear sets of equations: $$Ax+b=y$$

NumPy: conventional looping versus vector operations

Loop through your data and calculate mean and standard deviation (or regression, min, max, etc.).

vector = [1,2,3]
sum = 0
for element in vector:
    sum += element
mean = sum / len(vector)

import numpy as np
vector = np.array([1,2,3])
mean = np.sum(vector) / len(vector)

Numpy exercise 1

Use vectorized numpy operations to calculate standard deviation $$ \sigma = \sqrt{ \sum_{i=1..N} ( x_i - \mu )^2 / ( N - 1 ) } $$ where $N$ is the number of elements in $ \vec{x} $ and $ \mu $ is its mean.

Practice with team on whiteboard/laptop this and the two exercises below.

Numpy exercise 2

Use the dot product to calculate total miles covered by all cars:

• road_miles gives a list of different road segments and their lenght in miles.
• cars_roads give the number of cars that passed on each of the road segments.

Example:

road_miles = [108, 5, 10, 52]
cars_roads = [543, 433, 104, 390]

Numpy exercise 3

We expect the population to increase by 3% every year. Make a matrix of predictions for each county for the next three years by using:

• ga_population is a list of population numbers (in thousands) for each county.

Example:

# dekalb, fulton, gwinnett
ga_population = [757, 1065, 964]

Make a Colab notebook with your solution

• Do all 3 exercises individually
• Log into Google Colab with any Google account
• Create a new Python notebook
• Write some text and code blocks to explain your standard deviation code
• Compare your result to the output of np.std(vector, ddof=1) in your notebook
• Put additional blocks for exercise 2 and 3
• Click on Share and paste your link on Piazza

Pandas supports tabular data

• https://pandas.pydata.org/
• Akin to spreadseets and SQL tables
• Based on Numpy, but builds on it
• Primary components: Series and DataFrame
• Continue with Python for Data Analysis, chapter 5

Pandas objects:

• Series for 1-D data
• DataFrame for 2-D data
• Indexing (brackets, .loc, and .iloc)
• Filtering

Hands on activity

• Work in groups as before
• Use an online notebook; such as Google Colab - log in with any Google account
• Create a new Python notebook
• Create a Dataframe object from any data
• Extract a Series object from your DataFrame
  • Add a string index and show indexing example
  • Extract ndarray object and show indexing example
• Use slicing and fancy indexing to get subsets of your DataFrame
• Apply one comparison operator to use boolean indexing on your DataFrame
• Share your link on Piazza